Time Series

 

Time Series

  • Regression
  • White Noise
  • AutoRegression (AR)
  • Moving Average
  • ARMA
  • ARIMA
  • VAR

 

A time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Time series analysis comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Methods for time series analysis may be divided into two classes:

 

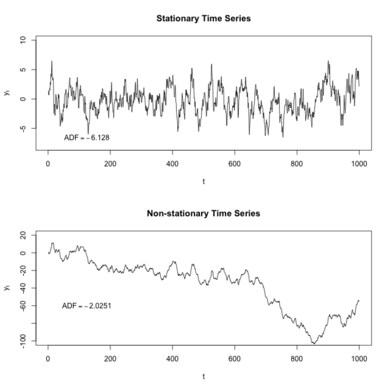
  • Stationarity
  • Seasonality
  • General Trend
  • Irregular Fluctuations

 

Stationarity is when data points have properties like mean, variance and autocorrelation that does not change over time == constant. Stationarity is an assumption underlying many statistical procedures in Time Series Analysis. Non-Stationary data is is unpredictable and cannot be modeled or forecasted. Non-stationary behaviors can be trends, cycles, random walks or combinations of these tree.
stationary time series and non stationary time series
No stationary data must almost always be transformed to become stationary either by:
  • Differencing: z[t] -z[t-1] (removing time trends)
  • Seasonal differencing: using lags
  • Fitting some type of curve and model the residuals from that fit (linear line)
  • Square or log the series

Pure Random Walk predicts the value at time t as the last value + stochastic component (white noise) that is independent and identically distributed with mean = 0 and variance σ² : Yt = Yt-1 + εt. It is a non mean reverting process that can be move a way from the mean in a positive or negative direction. The variance of a RW ⇒ ∞ as time ⇒ ∞ therefore a RW cannot be predicted.

Random Walk with Drift predicts the value at time t as the last value + a constant α + white noise ε with mean = 0 and variance σ² : Yt = α + Yt-1 + εt. So it is basically a Pure RW with a drift.

Deterministic Trend is just like a RW with drift but with regressed time trend βt instead of regressed on the last periods value Yt-1 so it looks like this: Yt = α +βt + εt

Random Walk with Drift and Deterministic Trend also non.stationary process that combines all of the above: Yt = α + Yt-1 +βt + εt

non-stationary financial time series data, we should distinguish between the different types of the non-stationary processes. This will provide us with a better understanding of the processes and allow us to apply the correct transformation. Read more: Introduction To Stationary And Non-Stationary Processes https://www.investopedia.com/articles/trading/07/stationary.asp#ixzz51oS9TaEd Follow us: Investopedia on Facebook Examples of non-stationary processes are random walk with or without a drift (a slow steady change) and deterministic trends (trends that are constant, positive or negative, independent of time for the whole life of the series). Read more: Introduction To Stationary And Non-Stationary Processes https://www.investopedia.com/articles/trading/07/stationary.asp#ixzz51oSCE2Rc Follow us: Investopedia on Facebook
  • White Noise (NM) model
    • simplest example of stationary process
    • a fixed, constant mean
    • a fixed, constant variance
    • no correlation over time
Seasonality or Trends means periodic fluctuations like e-commerce pre and post christmas. Seasonality is quite common in economic time series. It is less common in engineering and scientific data.
fgfg
fgfg
fgfg
fgfg
 Cycles

 

 

 

 

  • frequency-domain methods: spectral analysis and wavelet anaysis
  • time-domain methods: auto-correlation and cross-correlation analysis

 

 

 

 

  • ARIMA = AutoRegressive Integrated Moving Avergae
  • ARIMA(p,d,q) has 3 parts:
    • p: autoregressive order
    • d: order of integration (or difference)
    • q: moving average
    • ARIMA(0,0,0) is a white noise model WN

 

 

https://www.otexts.org/fpp2/ch-intro.html

https://pandas.pydata.org/pandas-docs/stable/timeseries.html

 

 

 

 

 

R:

  • ts
  • is.ts()
  • print(, type”b” or default type “l”)
  • length()
  • head()
  • tail()
  • start()
  • end()
  • time() vector of time, with one element for each time index on which the series was observed.
  • frequency()
  • deltat() fixed time intervall between observations
  • cycle()
  • plot()
  • ts.plot()
    • legend(“topleft”, colnames(data),  lty, col, bty)

ts(data, start=2001, frequency=1)

  • diff()
  • diff(lag = 12) monthly
  • diff(lag = 4) quartely
  • ts.plot(diff(data))

 

  • arima.sim(model = list(order = c(0,0,0)), n=50) simulate 50 obs from White Noise model
  • arima.sim(model = list(order = c(0,0,0)), n = 100, mean = 100, sd = 10)
  • arima(y, order = c(0,0,0)) fit wn model to y
  • arima.sim(model = list(order = c(0,1,0)), n=50) simulate 50 obs from Random Walk model
  • arima.sim(model = list(order = c(0,1,0)), n=50, mean = 1) simulate 50 obs from Random Walk model
    • mean argument = 1 to produce a drift