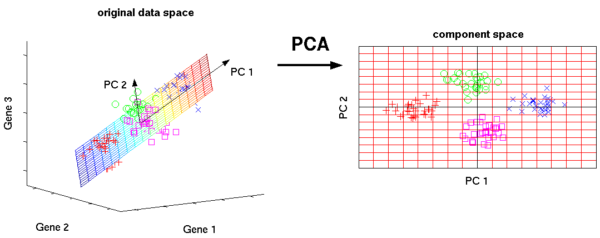
Principal Component Analysis

 

Principal Component Analysis (PCA)

Dimensionality reduction looks a lot like compression. This is about trying to reduce the complexity of the data while keeping as much of the relevant structure as possible

 

Cucumbers and iceberg lettuce contain of 96% water

 

  • A technique used to emphasize variation and bring out strong patterns in a dataset
  • Often used to make data easy to explore and visualize
  • Compressing data in some meaning-preserving way before feeding it to a deep neural net or another supervised learning algorithm.

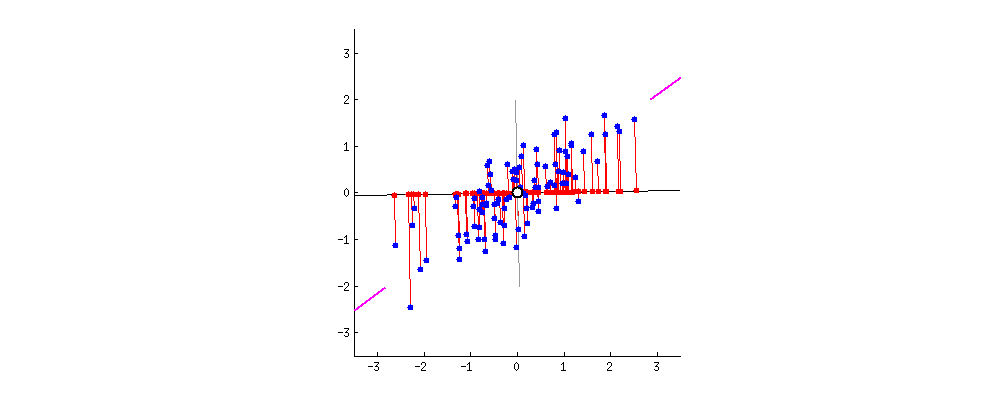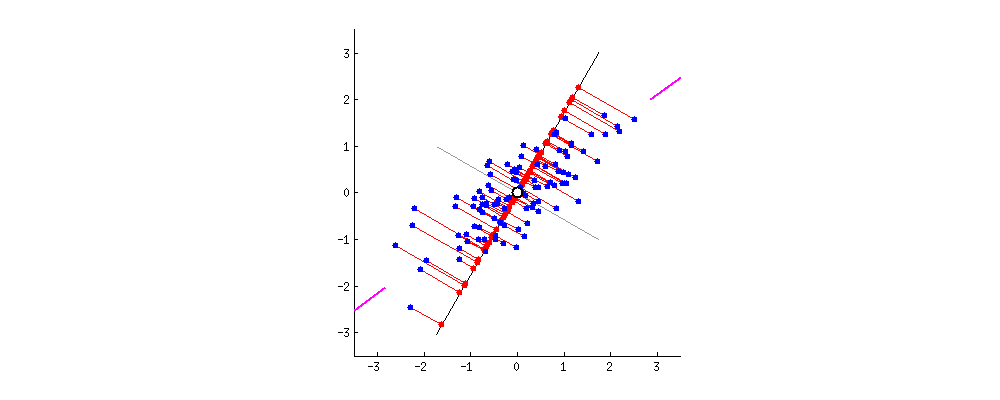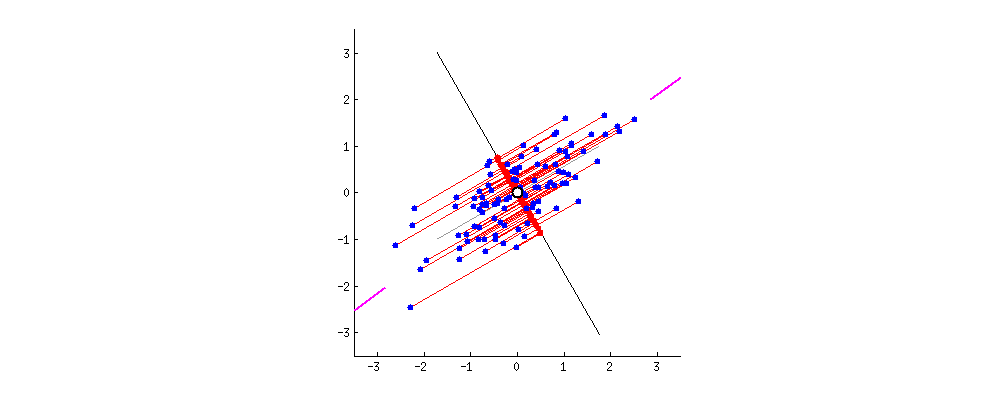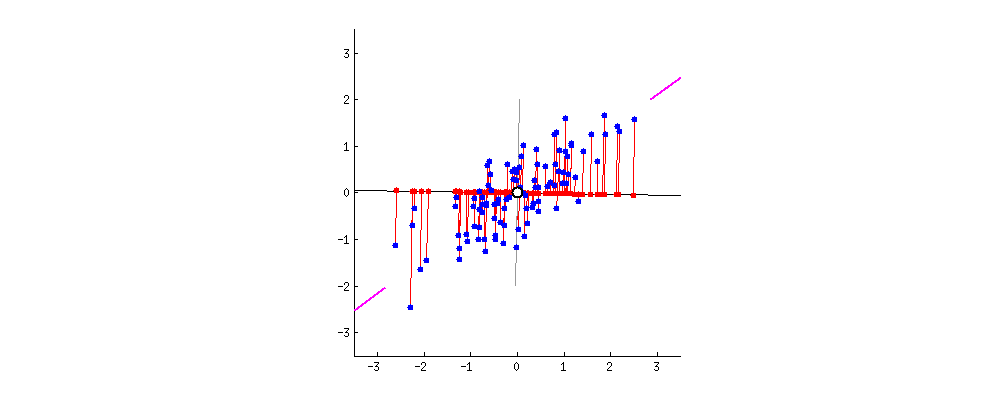
Come up with a basis for the space and then select only the most significant vectors that explain most of the space. These basis vectors are called principal components and the subset you select constitute a new space that is smaller in dimensionality than the original space but maintains as much of the complexity of the data as possible. To select the most significant principal components, we look at how much of the data’s variance they capture and order them by that metric.

Transformed dimension

The transformation definition makes sure that the principal components are ordered by variance so that by making use of the first several dimensions only, we can start gaining an understanding of the dataset’s organization.

 

http://setosa.io/ev/principal-component-analysis/

 

principal component analysis pca dimension reduction eigenvectors eigenvalues pca

 

PCA is more useful, because it's hard to see through a cloud of data. In the example below, the original data are plotted in 3D, but you can project the data into 2D through a transformation no different than finding a camera angle: rotate the axes to find the best angle. To see the "official" PCA transformation

 

PCA principal component analysis Principal component analysis (PCA) is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components. The number of distinct principal components is equal to the smaller of the number of original variables or the number of observations minus one. This transformation is defined in such a way that the first principal component has the largest possible variance

 

 

R:

pca1 <- princomp(X, scores = TRUE, cor = TRUE)
summary(pca1)
screeplot(pca1, type = ‘line’) #screeplot eigenvalues